Весовое среднее. Средняя квадратическая ошибка единицы веса и средняя квадратическая ошибка весового среднего.
Пусть имеем ряд равноточных измерений одной и той же величины, из которых образовано 3 группы:

Для каждой группы измерений можно получить среднее значение:
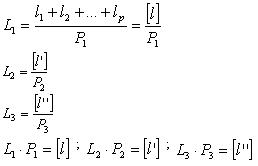
Результаты L1, L2, L3 – неравноточные, так как получены из разного числа измерений и имеют разные веса Р1, Р2, Р3.
Из первоначального ряда равноточных измерений можно найти арифметическую средину:
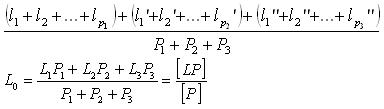
Эта формула представляет общую арифметическую средину или весовое среднее, получаемую из неравноточных измерений L1, L2, L3 с весами P1, P2, P3. Вес общей арифметической средины равен сумме весов.
Средние квадратические ошибки неравноточных измерений различны, поэтому для оценки точности таких измерений выбирают общую меру. Такой мерой является средняя квадратическая ошибка такого измерения, вес которого равен единице.
Следует отметить, что величина М (средняя квадратическая ошибка веса) может относится к воображаемому измерению, если среди результатов нет ни одного с весом равным единице.
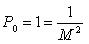
Установим связь между средней квадратической ошибкой единицы веса М и средней квадратической ошибкой результата измерений с весом

Для каждой группы измерений можно получить среднее значение:
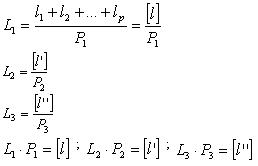
Результаты L1, L2, L3 – неравноточные, так как получены из разного числа измерений и имеют разные веса Р1, Р2, Р3.
Из первоначального ряда равноточных измерений можно найти арифметическую средину:
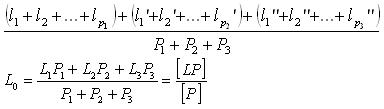
Эта формула представляет общую арифметическую средину или весовое среднее, получаемую из неравноточных измерений L1, L2, L3 с весами P1, P2, P3. Вес общей арифметической средины равен сумме весов.
Средние квадратические ошибки неравноточных измерений различны, поэтому для оценки точности таких измерений выбирают общую меру. Такой мерой является средняя квадратическая ошибка такого измерения, вес которого равен единице.
Следует отметить, что величина М (средняя квадратическая ошибка веса) может относится к воображаемому измерению, если среди результатов нет ни одного с весом равным единице.
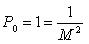
Установим связь между средней квадратической ошибкой единицы веса М и средней квадратической ошибкой результата измерений с весом
Чтобы увидеть самое интересное, Вам необходимо авторизоваться/зарегистрироваться
0 комментариев