Уравнивание систем нивелирных и теодолитных ходов с двумя узловыми точками способом приложений.
Этот способ применяется в тех случаях. когда исходные пункты находятся внутри сети или когда число полигонов более чем в полтора раза превышает число узловых точек. При этом способе получают последовательными приближениями неизвестные величины, связанные с узловыми точками.
В нивелирной сети известны высоты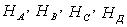 исходных пунктов, измеренные превышения по ходам
исходных пунктов, измеренные превышения по ходам 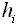 длины ходов
длины ходов 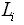 и число станций
и число станций 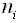 . Требуется найти высоты x, y и z узловых точек
. Требуется найти высоты x, y и z узловых точек 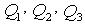 .
.
На основании метода наименьших квадратов можно составить систему уравнений с неизвестными высотами x, y и z и привести их к виду:
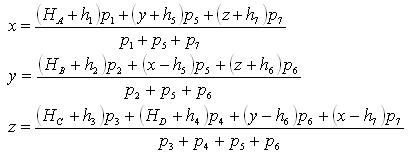
где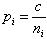 или
или 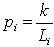 — вес измеренного превышения
— вес измеренного превышения 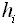 .
.
В качестве нулевых приближений, являющихся начальными, приняты произвольно выбранные числа. Но для того, чтобы процесс решения был более коротким, их получают путём передачи высот на узловые точки от ближайших исходных пунктов:
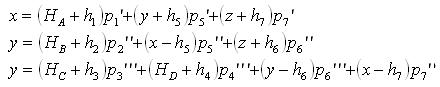
где,
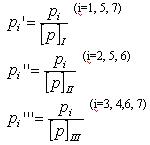
В нивелирной сети известны высоты
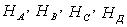 исходных пунктов, измеренные превышения по ходам
исходных пунктов, измеренные превышения по ходам 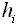 длины ходов
длины ходов 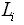 и число станций
и число станций 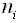 . Требуется найти высоты x, y и z узловых точек
. Требуется найти высоты x, y и z узловых точек 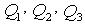 .
.На основании метода наименьших квадратов можно составить систему уравнений с неизвестными высотами x, y и z и привести их к виду:
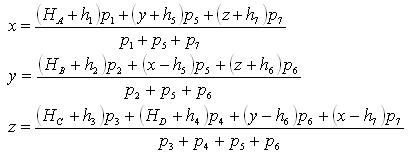
где
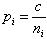 или
или 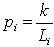 — вес измеренного превышения
— вес измеренного превышения 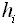 .
.В качестве нулевых приближений, являющихся начальными, приняты произвольно выбранные числа. Но для того, чтобы процесс решения был более коротким, их получают путём передачи высот на узловые точки от ближайших исходных пунктов:
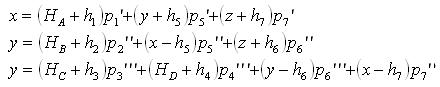
где,
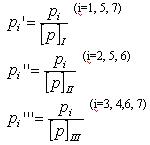
Чтобы увидеть самое интересное, Вам необходимо авторизоваться/зарегистрироваться
0 комментариев