Расчет необходимой и достаточной точности (принцип «равных влияний»).
В практике часто приходится решать задачу: задана определенная точность результата. Требуется определить с какой точностью должны быть получены результаты измерений, чтобы заданная точность была достигнута.
Эта задача решается по формуле:
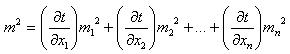
но величину (m) следует считать известной, а величины m1; m2; mn подлежат определению. При n > 1 задача неопределенна, то есть допускает бесчисленное число решений. Из которых можно выбрать наиболее выгодное, в частности пользуясь принципом равных влияний, то есть допускается, что ошибки m1; m2; mn одинаково влияют на величину m.
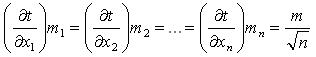
Написанное выражение определяет m1; m2; mn с точностью, с которой надо измерять х1, х2, хт.
Эта задача решается по формуле:
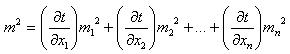
но величину (m) следует считать известной, а величины m1; m2; mn подлежат определению. При n > 1 задача неопределенна, то есть допускает бесчисленное число решений. Из которых можно выбрать наиболее выгодное, в частности пользуясь принципом равных влияний, то есть допускается, что ошибки m1; m2; mn одинаково влияют на величину m.
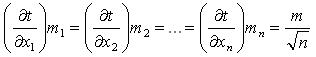
Написанное выражение определяет m1; m2; mn с точностью, с которой надо измерять х1, х2, хт.
0 комментариев