Формула Бесселя (средняя квадратическая ошибка по отклонениям от арифметической средины).
Формула Гаусса предполагает точное значение измеряемой величины.
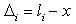
Так как величины всегда измеряют несколько раз, то всегда можно найти арифметическую средину:
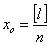
Можно также получить величины уклонений каждого измеренного значения от Х0, т.е получить ряд равенств:
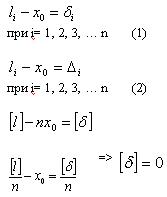
Вычтем из уравнения (2) уравнение (1), получим:
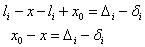
В левых частях уравнений стоят истинные ошибки арифметической средины. Заменим их СКО арифметической средины:
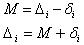
Возведем в квадрат и просуммируем:
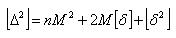
Разделим обе части на n:
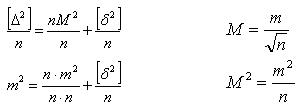
Формула Бесселя:
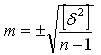
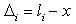
Так как величины всегда измеряют несколько раз, то всегда можно найти арифметическую средину:
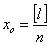
Можно также получить величины уклонений каждого измеренного значения от Х0, т.е получить ряд равенств:
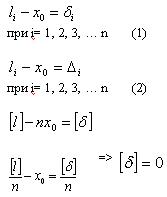
Вычтем из уравнения (2) уравнение (1), получим:
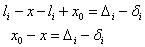
В левых частях уравнений стоят истинные ошибки арифметической средины. Заменим их СКО арифметической средины:
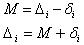
Возведем в квадрат и просуммируем:
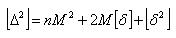
Разделим обе части на n:
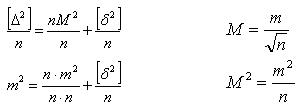
Формула Бесселя:
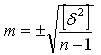
0 комментариев