Способ полигонов профессора Попова В.В. (способ красных чисел)
Способ проф. В.В. Попова применяется для уравнивания как свободной, так и несвободной сети полигонов.
Для нивелирной сети этот способ является строгим, т.е. дает такие же результаты, что и метод наименьших квадратов. Применительно же к сети теодолитных полигонов он не является строгим, поскольку при этом способе производится раздельное уравнивание углов и приращений координат.
Покажем сущность способа проф. В.В. Попова на примерах уравнивания различных сетей полигонов.
Уравнивание нивелирной сети
Рассмотрим сеть, состоящую из трех полигонов. На схематическом чертеже сети приводят все данные, необходимые для уравнивания, оценки точности и вычисления высот узловых точек — измеренные превышения hi, по каждому звену (ходу, связывающему две соседние узловые точки), длины звеньев Li — и число станций ni в каждом звене (стрелками показаны направления возрастания превышений) и отметка исходной марки.
Прежде всего подсчитывают невязки в превышениях по каждому полигону, соответствующие обходу полигона по направлению часовой стрелки, и их наибольшие по абсолютной величине допустимые значения. Результаты этих вычислений записывают на том же чертеже сети.
Убедившись в допустимости невязок, переходят к уравниванию сети. Для этой цели строят новый схематический чертеж сети крупных размеров, на котором непосредственно производится вычисление поправок на звенья.
На этом чертеже примерно в центре каждого полигона строят рамочки, над которыми римскими цифрами пишут номера полигонов, а внутри рамочек записывают невязки. Затем вне каждого полигона у каждого его звена строят рамочки для записи поправок. Таким образом, у внешних звеньев сети будет по одной рамочке, а у внутренних — по две (по одной с каждой стороны звена).
Для каждого звена полигона вычисляют красные числа ki, ki,j (i — номер данного полигона, j — номер смежного с ним). Красным числом называется отношение числа станций в звене к числу станций во всем полигоне (или отношение длины звена к периметру полигона).
Сумма красных чисел для каждого полигона должна быть равна единице (например, в первом полигоне 0,46 + 0,23 + + 0,31 = 1).
Полученные таким путем числа записывают красным цветом над соответствующими рамочками, расположенными вне полигона около его звеньев. Затем приступают к распределению невязок пропорционально красным числам соответствующих полигонов. Это распределение невязок производят непосредственно на чертеже сети, применяя при этом метод последовательных приближений.
Умножив невязку первого полигона (I) на его красные числа, полученные произведения, сумма которых должна быть равна распределяемой невязке (—25 — 12 — 17 = —54), записывают в соответствующих данному полигону рамочках. Распределенную невязку подчеркивают.
Переходят к полигону II. Здесь значение невязки изменится на величину поправки, перешедшей из полигона I (+38 — 12 == = +26). Учтенную поправку подчеркивают. Новую невязку распределяют пропорционально красным числам этого полигона (0,26; 0,46; 0,28) и полученные произведения (+7, +12, +7), сумма которых должна быть равна распределяемой невязке, записывают во внешних к полигону рамочках под соответствующими красными числами. Распределенную невязку подчеркивают.
В полигоне III будет новая невязка, равная сумме начальной невязки и поправок, перешедших из полигонов I и II (+36—17 + + 7 = +26). Учтенные поправки подчеркивают. Полученную невязку распределяют таким же путем, как и в первых двух полигонах, и подчеркивают.
Закончив распределение невязок во всех полигонах, возвращаются к полигону I. Здесь появится новая невязка, равная сумме поправок, перешедших из смежных полигонов. Эта невязка распределяется так же, как и первый раз.
Таким образом, закончив первый цикл распределения невязок, приступают ко второму, затем к третьему и так далее до тех пор, пока все невязки полигонов станут равными нулю.
Следует помнить, что во избежание повторного использования одной и той же величины в процессе распределения невязок каждое использованное значение необходимо сразу же подчеркнуть.
После того как все невязки будут распределены, подсчитывают суммы чисел во всех табличках у звеньев.
Правильность вычисления этих сумм контролируют по формулам. Расхождение при этом контроле не должно превышать 1,5 единицы последнего знака суммы.
Затем вычисляют поправки на звенья каждого полигона, считая направление звеньев совпадающим с направлением обхода полигона. Если i-й полигон по рассматриваемому звену не имеет смежного, то поправка на звено У, равна сумме чисел s,-внешней таблички этого звена с обратным знаком; если же по рассматриваемому звену полигон имеет смежный, то поправка на звено равна разности сумм чисел внутренней и внешней табличек этого звена.
Иначе говоря, чтобы получить поправки на звенья, внешние суммы полигона переносят внутрь полигона с противоположным знаком и складывают с его внутренними суммами для тех же звеньев, считая внутреннюю сумму равной нулю, если звено является внешним. Полученные поправки записывают в скобках около соответствующих звеньев. У внутренних звеньев сети по правки записывают по обе стороны звена (соответственно двум смежным полигонам этого звена).
В каждом полигоне сумма поправок на звенья должна равна невязке полигона с обратным знаком [например, для i полигона I: +14 +18 +22 = +54 = —(—54)].
Введя поправки в измеренные превышения, получают исправленные (уравненные) их значения, по которым вычисляют затем отметки узловых точек.
По поправкам на звеньях можно определить среднюю квадратическую погрешность нивелирования хода длиной 1 км по формуле:
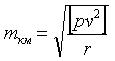
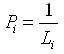
где, Li — длина звена, r — число полигонов.
Оценка точности будет надежна только в том случае, когда число полигонов r не слишком мало.
Если требуется вычислить высоты точек, расположенных внутри какого-либо звена, то производится уравнивание превышений в этом звене по правилу д одиночного хода.
Для нивелирной сети этот способ является строгим, т.е. дает такие же результаты, что и метод наименьших квадратов. Применительно же к сети теодолитных полигонов он не является строгим, поскольку при этом способе производится раздельное уравнивание углов и приращений координат.
Покажем сущность способа проф. В.В. Попова на примерах уравнивания различных сетей полигонов.
Уравнивание нивелирной сети
Рассмотрим сеть, состоящую из трех полигонов. На схематическом чертеже сети приводят все данные, необходимые для уравнивания, оценки точности и вычисления высот узловых точек — измеренные превышения hi, по каждому звену (ходу, связывающему две соседние узловые точки), длины звеньев Li — и число станций ni в каждом звене (стрелками показаны направления возрастания превышений) и отметка исходной марки.
Прежде всего подсчитывают невязки в превышениях по каждому полигону, соответствующие обходу полигона по направлению часовой стрелки, и их наибольшие по абсолютной величине допустимые значения. Результаты этих вычислений записывают на том же чертеже сети.
Убедившись в допустимости невязок, переходят к уравниванию сети. Для этой цели строят новый схематический чертеж сети крупных размеров, на котором непосредственно производится вычисление поправок на звенья.
На этом чертеже примерно в центре каждого полигона строят рамочки, над которыми римскими цифрами пишут номера полигонов, а внутри рамочек записывают невязки. Затем вне каждого полигона у каждого его звена строят рамочки для записи поправок. Таким образом, у внешних звеньев сети будет по одной рамочке, а у внутренних — по две (по одной с каждой стороны звена).
Для каждого звена полигона вычисляют красные числа ki, ki,j (i — номер данного полигона, j — номер смежного с ним). Красным числом называется отношение числа станций в звене к числу станций во всем полигоне (или отношение длины звена к периметру полигона).
Сумма красных чисел для каждого полигона должна быть равна единице (например, в первом полигоне 0,46 + 0,23 + + 0,31 = 1).
Полученные таким путем числа записывают красным цветом над соответствующими рамочками, расположенными вне полигона около его звеньев. Затем приступают к распределению невязок пропорционально красным числам соответствующих полигонов. Это распределение невязок производят непосредственно на чертеже сети, применяя при этом метод последовательных приближений.
Умножив невязку первого полигона (I) на его красные числа, полученные произведения, сумма которых должна быть равна распределяемой невязке (—25 — 12 — 17 = —54), записывают в соответствующих данному полигону рамочках. Распределенную невязку подчеркивают.
Переходят к полигону II. Здесь значение невязки изменится на величину поправки, перешедшей из полигона I (+38 — 12 == = +26). Учтенную поправку подчеркивают. Новую невязку распределяют пропорционально красным числам этого полигона (0,26; 0,46; 0,28) и полученные произведения (+7, +12, +7), сумма которых должна быть равна распределяемой невязке, записывают во внешних к полигону рамочках под соответствующими красными числами. Распределенную невязку подчеркивают.
В полигоне III будет новая невязка, равная сумме начальной невязки и поправок, перешедших из полигонов I и II (+36—17 + + 7 = +26). Учтенные поправки подчеркивают. Полученную невязку распределяют таким же путем, как и в первых двух полигонах, и подчеркивают.
Закончив распределение невязок во всех полигонах, возвращаются к полигону I. Здесь появится новая невязка, равная сумме поправок, перешедших из смежных полигонов. Эта невязка распределяется так же, как и первый раз.
Таким образом, закончив первый цикл распределения невязок, приступают ко второму, затем к третьему и так далее до тех пор, пока все невязки полигонов станут равными нулю.
Следует помнить, что во избежание повторного использования одной и той же величины в процессе распределения невязок каждое использованное значение необходимо сразу же подчеркнуть.
После того как все невязки будут распределены, подсчитывают суммы чисел во всех табличках у звеньев.
Правильность вычисления этих сумм контролируют по формулам. Расхождение при этом контроле не должно превышать 1,5 единицы последнего знака суммы.
Затем вычисляют поправки на звенья каждого полигона, считая направление звеньев совпадающим с направлением обхода полигона. Если i-й полигон по рассматриваемому звену не имеет смежного, то поправка на звено У, равна сумме чисел s,-внешней таблички этого звена с обратным знаком; если же по рассматриваемому звену полигон имеет смежный, то поправка на звено равна разности сумм чисел внутренней и внешней табличек этого звена.
Иначе говоря, чтобы получить поправки на звенья, внешние суммы полигона переносят внутрь полигона с противоположным знаком и складывают с его внутренними суммами для тех же звеньев, считая внутреннюю сумму равной нулю, если звено является внешним. Полученные поправки записывают в скобках около соответствующих звеньев. У внутренних звеньев сети по правки записывают по обе стороны звена (соответственно двум смежным полигонам этого звена).
В каждом полигоне сумма поправок на звенья должна равна невязке полигона с обратным знаком [например, для i полигона I: +14 +18 +22 = +54 = —(—54)].
Введя поправки в измеренные превышения, получают исправленные (уравненные) их значения, по которым вычисляют затем отметки узловых точек.
По поправкам на звеньях можно определить среднюю квадратическую погрешность нивелирования хода длиной 1 км по формуле:
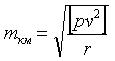
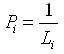
где, Li — длина звена, r — число полигонов.
Оценка точности будет надежна только в том случае, когда число полигонов r не слишком мало.
Если требуется вычислить высоты точек, расположенных внутри какого-либо звена, то производится уравнивание превышений в этом звене по правилу д одиночного хода.
0 комментариев