Средняя квадратическая ошибка функций измеренных величин.
В тех случаях когда искомая величина не может быть определена непосредственно, а вычисляется через измеренные величины, она является функцией измеренных величин. Например, в треугольнике ABC нет возможности измерить сторону ВС=а непосредственно. Однако измерив сторону АС=b,

и сторону ВС можно вычислить через измеренные величины. По теореме синусов имеем
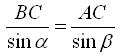
откуда
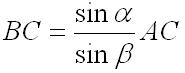
Так как сумма углов в треугольнике равна 180°, то можно угол β определить через непосредственно измеренные углы α и γ
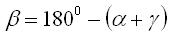
и тогда окончательно получим
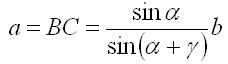
Сторона ВС является функцией измеренных величин α, γ, b. Формулы для оценки точности различного вида функций измеренных величин:
Произведение измеренной величины на постоянный множитель:
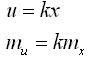
Сумма или разность двух измеренных величин:
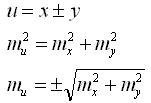
Алгебраическая сумма нескольких измеренных величин:
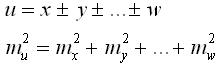
Линейная функция:
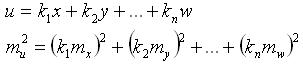
Функция общего вида:
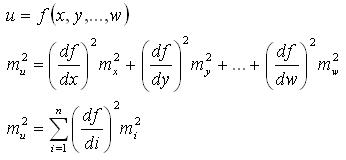

и сторону ВС можно вычислить через измеренные величины. По теореме синусов имеем
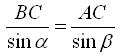
откуда
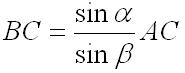
Так как сумма углов в треугольнике равна 180°, то можно угол β определить через непосредственно измеренные углы α и γ
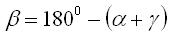
и тогда окончательно получим
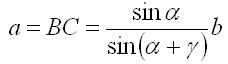
Сторона ВС является функцией измеренных величин α, γ, b. Формулы для оценки точности различного вида функций измеренных величин:
Произведение измеренной величины на постоянный множитель:
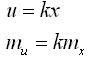
Сумма или разность двух измеренных величин:
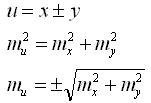
Алгебраическая сумма нескольких измеренных величин:
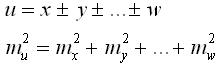
Линейная функция:
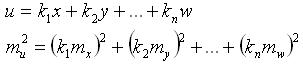
Функция общего вида:
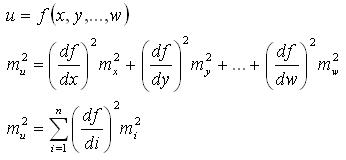
0 комментариев