Средняя квадратическая ошибка одного измерения.
Имея ряд измерений одной и той же величины мы должны уметь оценивать точность как 1 измерения, так и арифметической середины. Для оценки точности измерения применяют различные числовые характеристики. Одной из таких характеристик является средняя квадратическая ошибка Гаусса:

Следует помнить, что m не ошибка конкретного измерения, а средняя квадратическая величина таких ошибок. Казалось бы, что более естественно оценку точности выполнить так:
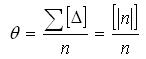
Однако, средняя квадратическая ошибка имеет ряд преимуществ, по сравнению с t, а именно на величину средней квадратической ошибки влияют большие по абсолютной величине ошибки.

Следует помнить, что m не ошибка конкретного измерения, а средняя квадратическая величина таких ошибок. Казалось бы, что более естественно оценку точности выполнить так:
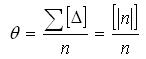
Однако, средняя квадратическая ошибка имеет ряд преимуществ, по сравнению с t, а именно на величину средней квадратической ошибки влияют большие по абсолютной величине ошибки.
Чтобы увидеть самое интересное, Вам необходимо авторизоваться/зарегистрироваться
0 комментариев