Свойства случайных ошибок.
Случайные ошибки характеризуются следующими свойствами.
1. При определенных условиях измерений случайные ошибки по абсолютной величине не могут превышать известного предела, называемого предельной ошибкой. Это свойство позволяет обнаруживать и исключать из результатов измерений грубые ошибки.
2. Положительные и отрицательные случайные ошибки примерно одинаково часто встречаются в ряду измерений, что помогает выявлению систематических ошибок.
3. Чем больше абсолютная величина ошибки, тем реже она встречается в ряде измерений.
4. Среднее арифметическое из случайных ошибок измерений одной и той же величины, выполненных при одинаковых условиях, при неограниченном возрастании числа измерений стремится к нулю. Это свойство, называемое свойством компенсации, можно математически записать так:
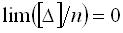
где [∆] — знак суммы, т.е.
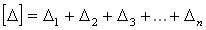
n — число измерений.
Последнее свойство случайных ошибок позволяет установить принцип получения из ряда измерений одной и той же величины результата, наиболее близкого к ее истинному значению, т.е. наиболее точного. Таким результатом является среднее арифметическое из n-измеренных значений данной величины. При бесконечно большом числе измерений n:
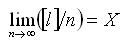
При конечном числе измерений арифметическая средина
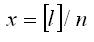
содержит остаточную случайную погрешность, однако от точного значения X измеряемой величины она отличается меньше, чем любой результат l непосредственного измерения. Это позволяет при любом числе измерений, если n>1, принимать арифметическую средину за окончательное значение измеренной величины. Точность окончательного результата тем выше, чем больше n.
1. При определенных условиях измерений случайные ошибки по абсолютной величине не могут превышать известного предела, называемого предельной ошибкой. Это свойство позволяет обнаруживать и исключать из результатов измерений грубые ошибки.
2. Положительные и отрицательные случайные ошибки примерно одинаково часто встречаются в ряду измерений, что помогает выявлению систематических ошибок.
3. Чем больше абсолютная величина ошибки, тем реже она встречается в ряде измерений.
4. Среднее арифметическое из случайных ошибок измерений одной и той же величины, выполненных при одинаковых условиях, при неограниченном возрастании числа измерений стремится к нулю. Это свойство, называемое свойством компенсации, можно математически записать так:
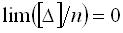
где [∆] — знак суммы, т.е.
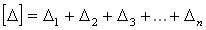
n — число измерений.
Последнее свойство случайных ошибок позволяет установить принцип получения из ряда измерений одной и той же величины результата, наиболее близкого к ее истинному значению, т.е. наиболее точного. Таким результатом является среднее арифметическое из n-измеренных значений данной величины. При бесконечно большом числе измерений n:
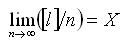
При конечном числе измерений арифметическая средина
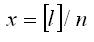
содержит остаточную случайную погрешность, однако от точного значения X измеряемой величины она отличается меньше, чем любой результат l непосредственного измерения. Это позволяет при любом числе измерений, если n>1, принимать арифметическую средину за окончательное значение измеренной величины. Точность окончательного результата тем выше, чем больше n.
0 комментариев