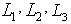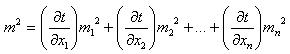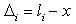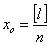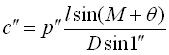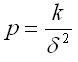Для вычисления прямоугольных координат по географическим используют таблицы Гаусса-Крюгера для широт от 32º до 80º через 5’ и для долгот от 0º до 6º через 7,5’.
Основным назначением таблиц является использование их для построения в проекции Гаусса-Крюгера рамок трапеции карт и координатных сеток. В таком случае долготы l=L-L0 западной и восточной трапеции относительно осевого меридиана зоны будут: -2º52’30’’ и -2º45’. Из таблиц выбираем значения координат Гаусса-Крюгера и гауссово сближение меридианов. Вычисления выполняются по схеме, при этом условные координаты определяются путем прибавления 500 км.
Читать дальше →
Этот способ применяется в тех случаях. когда исходные пункты находятся внутри сети или когда число полигонов более чем в полтора раза превышает число узловых точек. При этом способе получают последовательными приближениями неизвестные величины, связанные с узловыми точками.
В нивелирной сети известны высоты
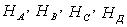
исходных пунктов, измеренные превышения по ходам
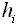
длины ходов
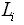
и число станций
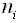
. Требуется найти высоты x, y и z узловых точек
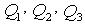
.
Читать дальше →
Пусть требуется уровнять систему из 3-х нивелирных ходов.
Дано:
Суммарные превышения по ходам
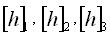
;
Длины ходов в км
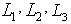 Читать дальше →
Читать дальше →
В практике часто приходится решать задачу: задана определенная точность результата. Требуется определить с какой точностью должны быть получены результаты измерений, чтобы заданная точность была достигнута.
Эта задача решается по формуле:
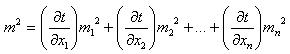 Читать дальше →
Читать дальше →
Формула Гаусса предполагает точное значение измеряемой величины.
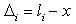
Так как величины всегда измеряют несколько раз, то всегда можно найти арифметическую средину:
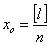 Читать дальше →
Читать дальше →
Если при измерении горизонтальных направлений теодолит был установлен не над центром знака, то в измеренные направления вводят исправления, называемые поправками за центрировку. Их величину подсчитывают по формуле:
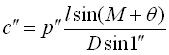 Читать дальше →
Читать дальше →
Способ проф. В.В. Попова применяется для уравнивания как свободной, так и несвободной сети полигонов.
Для нивелирной сети этот способ является строгим, т.е. дает такие же результаты, что и метод наименьших квадратов. Применительно же к сети теодолитных полигонов он не является строгим, поскольку при этом способе производится раздельное уравнивание углов и приращений координат.
Покажем сущность способа проф. В.В. Попова на примерах уравнивания различных сетей полигонов.
Читать дальше →
Если результаты измерений получены не в одинаковых условиях и им соответствуют различные дисперсии, а следовательно, и средние квадратические погрешности, то измерения называются неравноточными.
При обработке неравноточных измерений вводят новую характеристику точности измерения, называемую весом измерения.
Вес результата измерения
р определяется формулой:
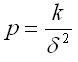 Читать дальше →
Читать дальше →
Часто приходится производить оценку точности арифметической средины

полученной по формуле из ряда равноточных измерений
l1,l2,...ln.
L является функцией вида
n=kx1+kx2+...+kxn.
При
k=1/n и равноточных измерениях, когда
Читать дальше →
Для того, чтобы сделать сайт более интересным и полезным для вас, мне необходимо узнать какие интересующие вас темы вы не смогли найти на сайте. Для этого предлагаю оставлять в комментариях к этой теме сообщения с пожеланиями и вопросами.
Буду благодарен, если в этом сообщении вы укажете:
1) являетесь ли студентом,
2) факультет и специальность обучения,
3) если вы работаете, то укажите свой вид деятельности.




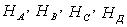 исходных пунктов, измеренные превышения по ходам
исходных пунктов, измеренные превышения по ходам 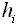 длины ходов
длины ходов 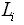 и число станций
и число станций 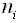 . Требуется найти высоты x, y и z узловых точек
. Требуется найти высоты x, y и z узловых точек 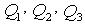 .
.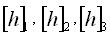 ;
;